Machine Learning

Introducción

Los términos machine learning y aprendizaje automático se utilizan indistintamente.

Inteligencia artificial

Aunque a veces se usan indistintamente los términos inteligencia artificial y machine learning, machine learning es solo una parte de la inteligencia artificial.

Ejemplos en los que se utiliza hoy en día la inteligencia artificial son:

• Detección del fraude.
• Programación de recursos.
• Análisis complejo.
• Automatización.
• Atención al cliente.
• Sistemas de seguridad.
• Eficiencia y control de la maquinaria.

Ejemplos en los que se utiliza aprendizaje automático:

• Control de accesos.
• Protección animal.
• Predicción de tiempos de espera.

El aprendizaje automático permite que la inteligencia artificial desarrolle estas tareas:

• Adaptarse a nuevas circunstancias.
• Detectar patrones en fuentes de datos.
• Crear nuevos comportamientos basados en los patrones reconocidos.
• Tomar decisiones basados en los aciertos o errores de dichos comportamientos.

El uso de algoritmos para manipular datos es el centro del aprendizaje automático. El aprendizaje automático intenta descifrar los datos buscando patrones en los mismos.

Además del aprendizaje automátivo, la inteligencia artificial incluye:

• Procesamiento del lenguaje natural.
• Comprensión del lenguaje natural.
• Representación del conocimiento.
• Planificación (búsqueda de objetivos).
• Robótica.

Big Data

Big data no solo se refiere a grandes cantidades de datos, sino a que estos datos incluyan cierta complejidad.

Cuantos más datos obtengamos, más fácilmente podremos diferenciar patrones válidos de patrones debidos a irregularidades o errores. Sin embargo, cuando el tamaño de los conjuntos de datos aumenta considerablemente, muchas de las técnicas más tradicionales de aprendizaje automático no resultan adecuadas por ser ineficientes y poco escalables. La necesidad de trabajar eficientemente con grandes conjuntos de datos dio lugar al desarrollo de la minería de datos, o data mining.

La minería de datos es el subconjunto de las técnicas de aprendizaje automático que se pueden aplicar a conjuntos de datos enormes. Para ello, las técnicas de aprendizaje se suelen combinar con métodos estadísticos y con técnicas de bases de datos que hagan posible el análisis de cantidades ingentes de datos. Esta disciplina se conoce como big data.

Aprendizaje automático

El aprendizaje automático (o machine learning) es una rama de la computación que se encarga de construir algoritmos que se basan en el tratamiento de una colección de ejemplos; estos ejemplos pueden provenir de la naturaleza, ser aportados de forma manual o generados por otros algoritmos.

También se puede definir el aprendizaje automático como el proceso de resolver un problema práctico mediante:

1. recopilar un conjunto de datos,
2. construir algorítmicamente un modelo estadístico basado en ese conjunto de datos,
3. este modelo estadístico se utilizará de alguna forma para resolver el problema práctico.

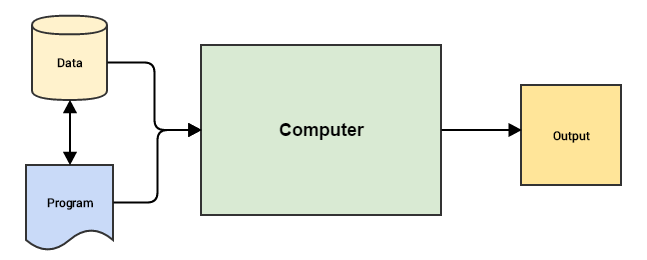
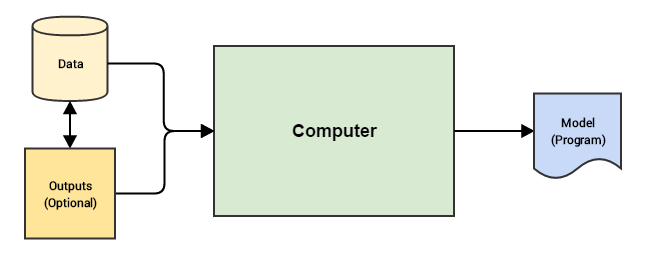
A continuación se muestran las diferencias entre la programación tradicional y el aprendizaje automático:

Programación tradicional

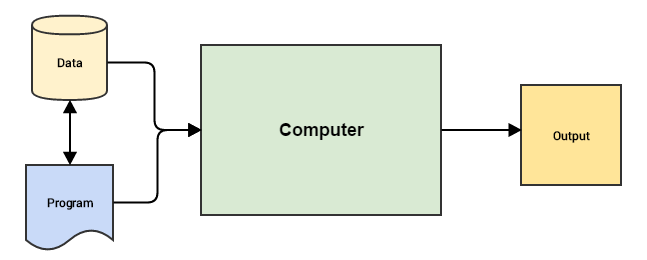
Machine Learning

Aplicaciones del aprendizaje automático

El uso de técnicas de aprendizaje automático es recomendable en las tareas que nos gustaría poder automatizar, pero no hemos sido capaces de hacerlo por la complejidad que requeriría la programación de algoritmos tradicionales para resolver los problemas asociados a ellas. Se trata de problemas que nosotros resolvemos con relativa facilidad, pero son extremadamente difíciles de resolver utilizando un algoritmo secuencial diseñado manualmente.

La tareas más populares dentro del Machine Learning son

• clasificación,
• regresión,
• detección de anomalías,
• anotación estructurada,
• traducción,
• agrupación,
• transcripción.

Disciplinas relacionadas con Machine Learning

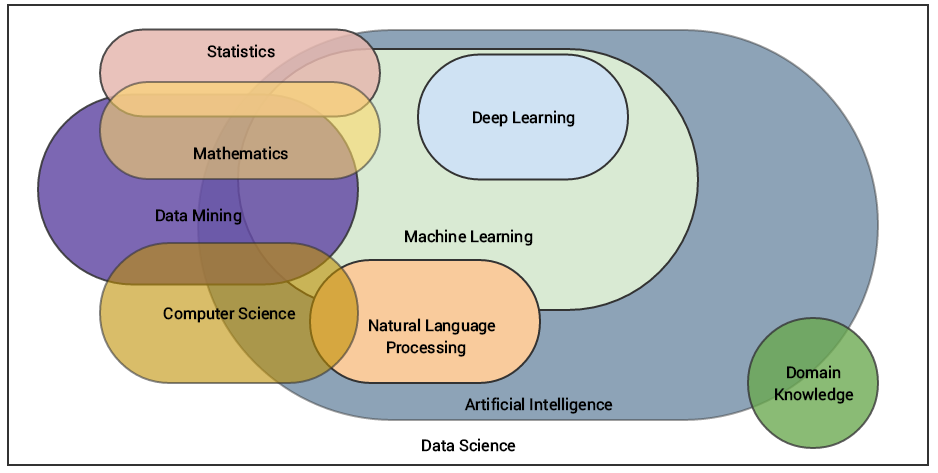
Tipos de aprendizaje automático

El aprendizaje automático puede ser -dependiendo del algoritmo y de sus objetivos- supervisado, semi-supervisado, no supervisado y por refuerzo.

Aprendizaje supervisado

El aprendizaje supervisado se da cuando un algoritmo aprende de los datos ejemplo y respuestas objetivo, para predecir más tarde la respuesta correcta con nuevos ejemplos. Es similar al aprendizaje humano bajo la supervisión de un profesor: el profesor da ejemplos al alumno y éste obtiene reglas genéricas a partir de estos ejemplos.

Se distingue entre problemas de regresión, cuyo objetivo es un valor numérico; y problemas de clasificación, cuyo objetivo es una clase o etiqueta.

Aprendizaje no supervisado

El aprendizaje no supervisado se da cuando un algoritmo aprende de ejemplos planos sin ninguna respuesta asociada, dejando al algoritmo determinar por sí mismo los patrones. Es similar a los métodos que usamos los humanos para descifrar si ciertos objetos o eventos son de la misma clase buscando un grado de similitud entre ellos.

Clustering

La variante más conocida de las técnicas de aprendizaje no supervisado es la formada por los métodos de agrupamiento o clustering.

Aprendizaje por refuerzo

En el aprendizaje por refuerzo se le aportan al algoritmo ejemplos sin etiquetar, igual que se hace en el aprendizaje no supervisado. Sin embargo, según la solución que proponga el algoritmo se puede dar un feedback positivo o negativo. Se asemeja al aprendizaje humano por prueba y error.

El proceso de aprendizaje

Aunque el aprendizaje supervisado es el más popular y el más utilizado de los tres tipos, todos los algoritmos de aprendizaje responden a la misma lógica. La idea central es representar la realidad usando una función matemática que no conoce el algoritmo de antemano, pero que puede adivinar a partir de algunos datos.

Aprendizaje automático supervisado

Los sistemas de AA (Aprendizaje Automático) aprenden cómo combinar entradas para producir predicciones útiles sobre datos nunca antes vistos.

El aprendizaje automático proporciona mecanismos mediante los cuales el ordenador es capaz de aprender por sí mismo a resolver un problema. El programador se encarga de diseñar un algoritmo de aprendizaje que resulte adecuado para el problema que se pretende resolver, pero es el ordenador el que resuelve el problema, aprovechando para ellos los datos a los que tenga acceso y las heurísticas de aprendizaje incorporadas.

Para que el aprendizaje automático sea correcto hemos de disponer de suficientes casos de entrenamiento. Si las conclusiones obtenidas no vienen avaladas por un número suficiente de ejemplos, entonces la aparición de errores o ruido en los datos podría conducir al aprendizaje de un modelo erróneo.

Definiciones

• Una etiqueta es el valor que estamos prediciendo, es decir la variable $y$ en la regresión lineal simple.
• Un atributo es la variable de entrada, es decir la variable $x$ en la regresión lineal simple.
• Un ejemplo es una instancia de datos en particular $\vec{x}$. Los ejemplos pueden ser etiquetados o ejemplos sin etiqueta.
  • Un ejemplo etiquetado incluye tanto atributos como la etiqueta, y se usan para entrenar el modelo.
  • Un ejemplo sin etiqueta incluye atributos pero no la etiqueta. Una vez que el modelo se ha entrenado con ejemplos etiquetados se utiliza para predecir la etiqueta en ejemplos sin etiqueta.
• Un modelo define la relación entre los atributos y la etiqueta. En el ciclo de un modelo destacan dos fases:
  • Entrenamiento significa crear o aprender el modelo.
  • Inferencia significa aplicar el modelo entrenado a ejemplos sin etiqueta.
• Un modelo de regresión predice valores continuos.
• Un modelo de clasificación predice valores discretos.

Aplicaciones del aprendizaje supervisado

• Sistemas de recuperación de la información (information retrieval).
• Sistemas de pregunta-respuesta o sistema QA (question answering).
• Sistemas de recomendación (recommender systems).

Entrenamiento y pérdida

Entrenar un modelo significa aprender (determinar) valores correctos para todas las ponderaciones y las ordenadas al origen de los ejemplos etiquetados. En un aprendizaje supervisado el algoritmo de un aprendizaje automático construye un modelo al examinar varios ejemplos intentando minimizar la pérdida (minimización del riesgo empírico).

La pérdida es una penalización por una predicción incorrecta. Si la predicción fuera perfecta, la pérdida sería cero, en caso contrario será un número positivo.

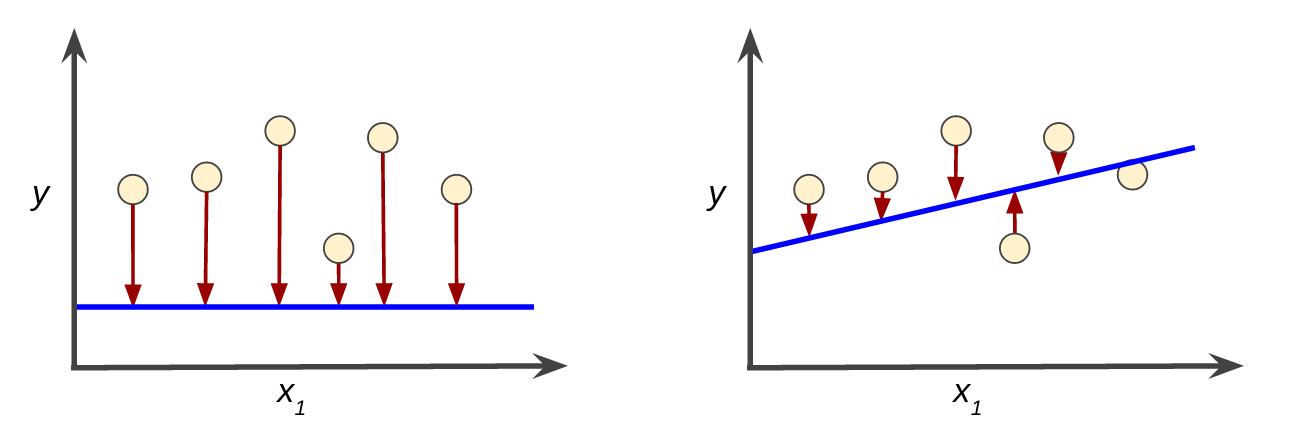
El objetivo de entrenar un modelo es encontrar un conjunto de ponderaciones y ordenadas al origen que, en promedio, tengan pérdidas bajas en todos los ejemplos.

Pérdida alta en el modelo de la izquierda; pérdida baja en el modelo de la derecha

Funciones de pérdida

Pérdida al cuadrado ($L_2$)

$$
L_2 = (y-y’)^2
$$

Error cuadrático medio (ECM)

$$
ECM = \frac{1}{N} \sum_{(x,y)\in D} (y – \textrm{predicción}(x) )^2
$$

Reducción de la pérdida

Los algoritmos de aprendizaje automático utilizan un proceso iterativo de prueba y error para entrenar un modelo:

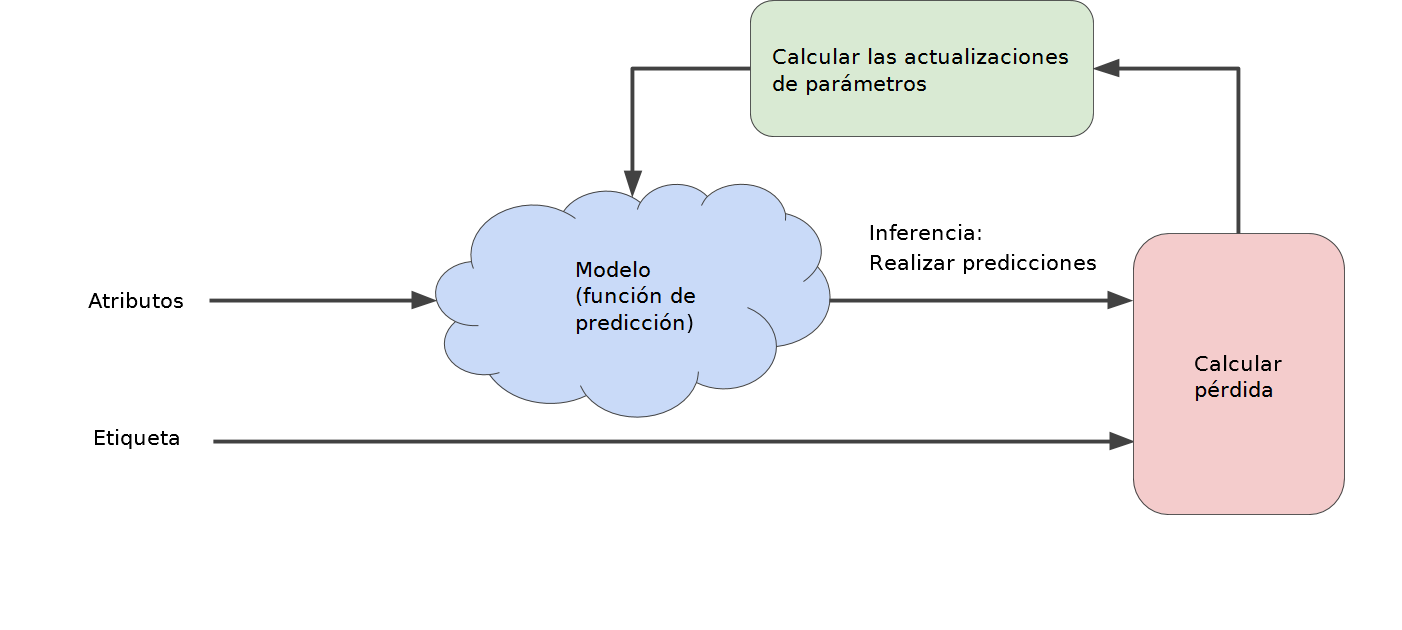
Las estrategias iterativas prevalecen en ya que se ajustan muy bien a los conjuntos de datos de gran tamaño.

La iteración se realiza hasta que la pérdida general deja de cambiar o, al menos, cambia muy lentamente. Cuando eso ocurre se dice que el modelo ha convergido.

Un modelo de aprendizaje automático se entrena comenzando con una hipótesis inicial para los pesos y sesgo, y de manera iterativa se ajustan esas hipótesis hasta que se aprenden las ponderaciones y ordenadas al origen con la pérdida más baja posible.

Descenso de gradientes

El gradiente de una función ($\nabla f$) es el vector de las derivadas parciales con respecto a todas las variables independientes.

Por ejemplo, si

$$
f(x,y) = e^{xy}sin(x)
$$

entonces

$$
\nabla f(x,y) = (\frac{\partial f}{\partial x}(x,y), \frac{\partial f}{\partial y}(x,y) ) = (e^{2y}cos(x), 2e^{2y} sin(x))
$$

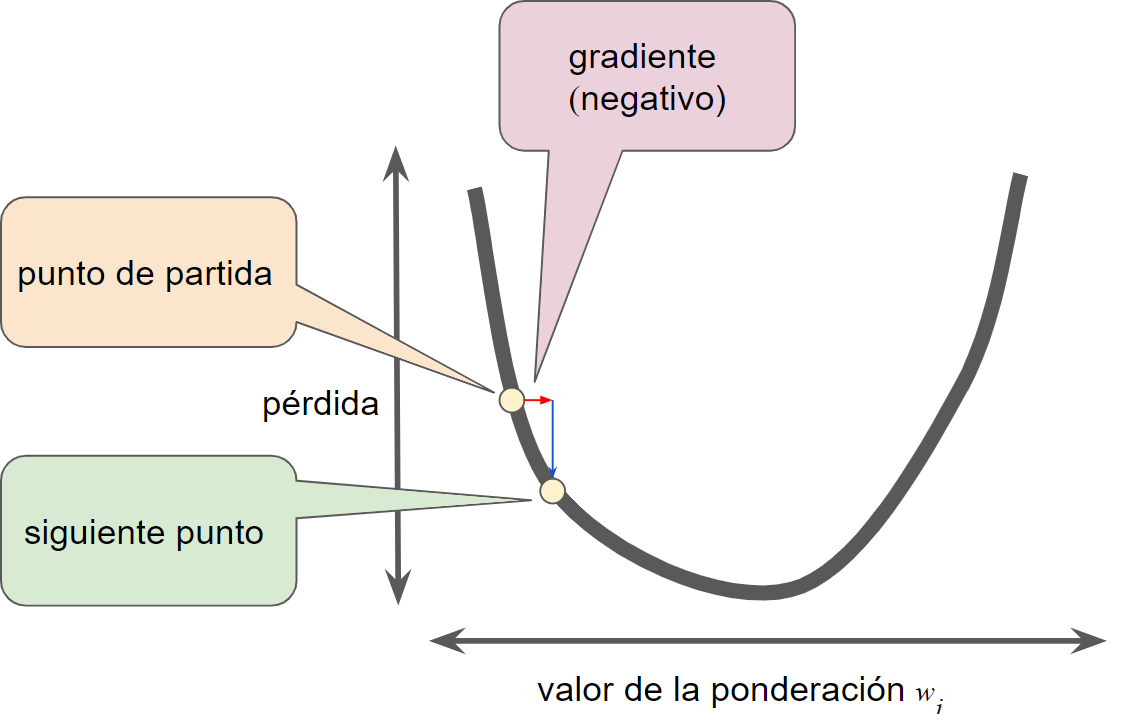
El gradiente siempre apunta en la dirección del aumento más empinado de la función de pérdida. Por lo tanto, el algoritmo de descenso de gradientes sigue estos pasos:

1. El algoritmo toma un paso en dirección de el gradiente negativa para reducir la pérdida lo más rápido posible.
2. Para determinar el siguiente punto a lo largo de la curva de la función de pérdida, el algoritmo de descenso de gradientes agrega alguna función de la magnitud de el gradiente al punto de partida.
3. Luego el descenso de gradientes repite este proceso y se acerca cada vez más al mínimo.

Tasa de aprendizaje

Los algoritmos de descenso de gradientes multiplican el gradiente por un escalar conocido como tasa de aprendizaje (o tamaño del paso) para determinar el siguiente punto.

Por ejemplo, si la magnitud de el gradiente es 2.5 y la tasa de aprendizaje es 0.01, el algoritmo de descenso de gradientes tomará el siguiente punto 0.025 más alejado del punto anterior.

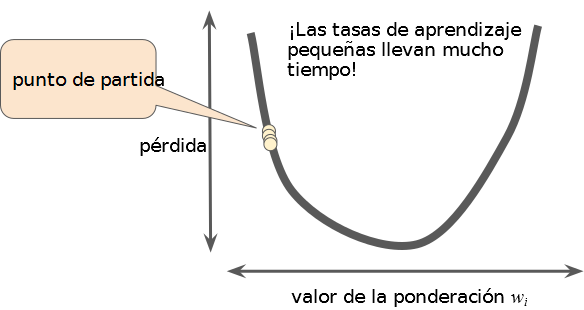
Si se elige una tasa de aprendizaje muy pequeña el aprendizaje llevará demasiado tiempo. Al contrario, si se elige una tasa de aprendizaje muy grande el siguiente punto rebotará al azar eternamente en la parte inferior.

Hay una tasa de aprendizaje ideal (con valor dorado) para cada problema de regresión. El valor dorado está relacionado con cómo es de plana la función de pérdida.

Tasa de aprendizaje demasiado pequeña

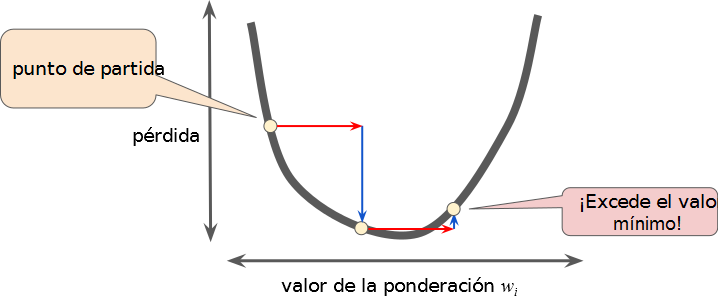
Tasa de aprendizaje demasiado grande

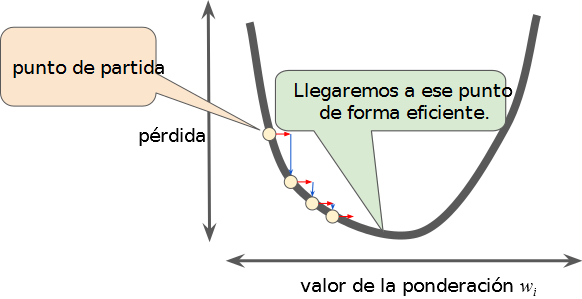
Tasa de aprendizaje correcta

Descenso de gradiente estocástico

Un lote es la cantidad total de ejemplos que se usan para calcular el gradiente en un sola iteración. Un lote de datos muy grande puede hacer que una sola iteración tome un tiempo muy prolongado para calcularse.

El descenso de gradiente estocástico (SGD) usa un solo ejemplo (un lote de tamaño 1) por iteración, este ejemplo se elige al azar. Cuando se dan muchas iteraciones el SGD funciona, pero es muy inconsistente.

El descenso de gradiente estocástico de minilote es un equilibrio entre la interación de bloque completo y el SGD. Un minilote suele tener entre 10 y 1000 ejemplos, elegidos al azar. El SGD de minilote reduce la inconsistencia del SGD, pero sigue siendo más eficaz que el lote completo.

TensorFlow

Toolkit

La jerarquía actual del toolkit de TensorFlow es la siguiente:

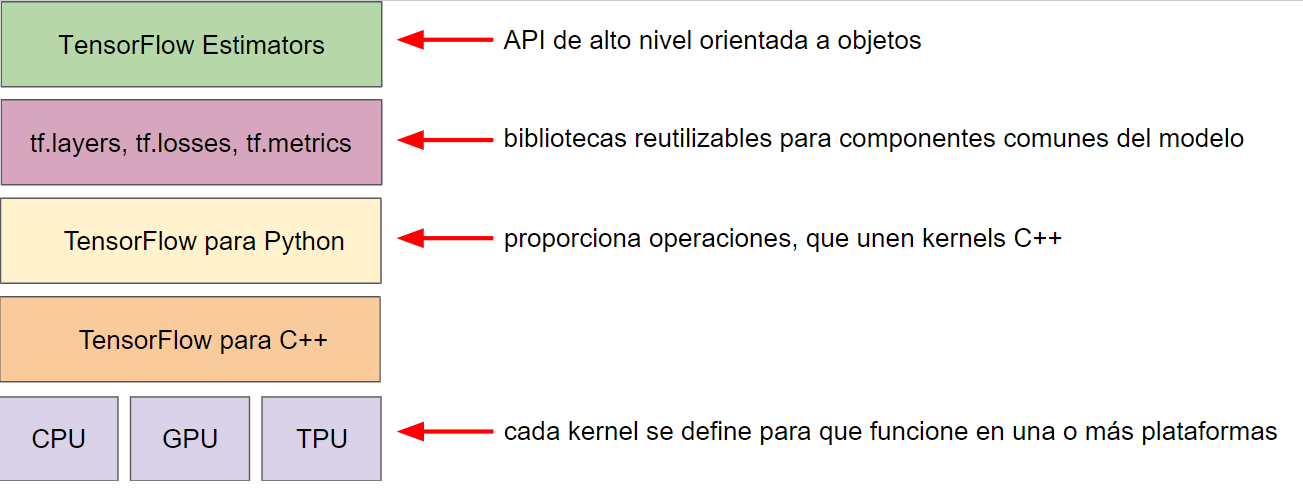
Los objetivos de las siguientes capas son:

Toolkit	Descripción
Estimador (tf.estimator)	API de POO de alto nivel
tf.layers, tf.losses, tf.metrics	bibliotecas de componentes comunes del modelo
TensorFlow	API de nivel inferior

TensorFlow consiste en los siguientes dos componentes:

• Un búfer de protocolos de grafo
• Un tiempo de ejecución que ejecuta el grafo (distribuido)

Estos dos componentes son análogos al compilador de Java y a la JVM.

Se debe usar el nivel de abstracción más alto que resuelva el problema. Los niveles de abstracción más altos son más fáciles de usar pero también menos flexibles.

API de tf.estimator

tf.estimator es compatible con la API de scikit-learn, biblioteca de aprendizaje automático de código abierto en Python.

Ejemplo de programa de regresión lineal implementado en tf.estimator:

import tensorflow as tf

## Establece un clasificador lineal.
classifier = tf.estimator.LinearClassifier()

## Entrena el modelo en algunos datos ejemplo.
classifier.train(input_fn=train_input_fn, steps=2000)

## Lo usa para predecirlo.
predictions = classifier.predict(input_fn=predict_input_fn)

Redes neuronales

Las redes neuronales se utilizan para el aprendizaje profundo, o Deep Learning.

Referencias

• Practical Machine Learning with Python, Dipanjan Sarkar, Tushar Sharma y Raghav Bali
• Google – Curso introductorio
• The Hundred-Page Machine Learning Book, Andriy Burkov
• Machine Learning For Dummies, John Paul Mueller y Luca Massaron