Descenso del gradiente

IA

El método del descenso del gradiente (gradient descent) es un algoritmo de optimización que permite converger hacia el valor mínimo de una función mediante un proceso iterativo.

En aprendizaje automático básicamente se utiliza para minimizar una función que mide el error de predicción del modelo en el conjunto de datos. A esta función se le denomina función de coste, $J(\Theta)$.

El algoritmo básico del método del descenso del gradiente es:

  1. Inicializar los parámetros de $\Theta$ a un valor de inicio.
  2. Indicar la valor de velocidad de aprendizaje del algoritmo, $\alpha$.
  3. Obtener la derivada de $J$ en el punto $\Theta$.
  4. Sustraer la derivada por la velocidad de aprendizaje al valor actual del parámetro.
  5. Actualizar el valor de $\Theta$.
  6. Si el cambio en la actualización de los parámetros en inferior a uno fijado previamente, el criterio de parada, finalizar la ejecución.
  7. En caso contrario volver al punto 3.

Ejemplo en Python

De analyticslane

import numpy as np

# Creación de un conjunto de datos para entrenamiento
trX = np.linspace(-2, 2, 101)
trY = 3 + 2 * trX + np.random.randn(*trX.shape) * 1.3

# Definición de los ajustes y parámetros iniciales
num_steps = 100
learningRate = 0.10
criteria = 1e-8
b_0 = 1
b_1 = 1

# Proceso iterativo
for step in range(0, num_steps):
    b_0_gradient = 0
    b_1_gradient = 0
    N = float(len(trX))

    for i in range(0, len(trX)):
        b_0_gradient -= (2/N) * (trY[i] - (b_0 + b_1 * trX[i]))
        b_1_gradient -= (2/N) * (trY[i] - (b_0 + b_1 * trX[i])) * trX[i]
        
    b_0 = b_0 - (learningRate * b_0_gradient)
    b_1 = b_1 - (learningRate * b_1_gradient)

    if max(abs(learningRate * b_0_gradient), abs(learningRate * b_1_gradient)) < criteria:
        break
    
# Impresión de los resultados
print("Los valores que se obtienen son:", b_0, b_1, "en pasos", step)

Los valores que se obtienen son: 2.9151310528407275 1.8706427810269992 en pasos 79

En este ejemplo se ha implementado el método para una regresión lineal. En las primeras líneas se crea un conjunto de datos en la que los puntos se corresponde con una recta de parámetros 2 y 3 al que se ha añadido ruido aleatorio. Posteriormente se define el número máximo de veces que se va a iterar, la ratio de aprendizaje, el criterio de parada y los valores iniciales para los parámetros.

Posteriormente se implementa el modelo. En primer lugar, se ha de obtener el valor del gradiente, para ello se utilizan las derivadas parciales de la función de coste respecto a los parámetros. Para el primer y segundo parámetro son respectivamente

$$
\frac{\partial E(\beta_0,\beta_1)}{\partial \beta_0} = – \frac{2}{N} \sum_{i=1}^N \left(y_i -(\beta_0 + \beta_1 x_i) \right)
$$

y

$$
\frac{\partial E(\beta_0,\beta_1)}{\partial \beta_1} = – \frac{2}{N} \sum_{i=1}^N x_i \left(y_i -(\beta_0 + \beta_1 x_i) \right)
$$

El gradiente indica la dirección y la intensidad en la que se han de mover los valores para minimizar la función de coste. Esto se puede hacer respectivamente mediante

$$
\beta_0 = \beta_0 – l_r \frac{\partial E(\beta_0,\beta_1)}{\partial \beta_0}
$$

y

$$
\beta_1 = \beta_1 – l_r \frac{\partial E(\beta_0,\beta_1)}{\partial \beta_1}
$$

Al finalizar se muestran los resultados. Los parámetros y el número de pasos necesarios para llegar al objetivo.

Finalmente se pueden comparar gráficamente los resultados con los datos utilizados. En esta gráfica se puede ver cómo se ajusta el modelo a los datos utilizados.

# Visualización
import matplotlib.pyplot as plt

Y = b_1 * trX + b_0
plt.scatter(trX,trY)
plt.plot(trX, Y, color='red');

Otro ejemplo de implementación

1. Implementación del algoritmo de descenso de gradiente

Se va a implementar las funciones básicas del algoritmo de descenso de gradiente para encontrar el límite en un conjunto de datos pequeño. Primero, comenzaremos con algunas funciones que nos ayudarán a trazar y visualizar los datos.

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd

#Some helper functions for plotting and drawing lines

def plot_points(X, y):
    admitted = X[np.argwhere(y==1)]
    rejected = X[np.argwhere(y==0)]
    plt.scatter([s[0][0] for s in rejected], [s[0][1] for s in rejected], s = 25, color = 'blue', edgecolor = 'k')
    plt.scatter([s[0][0] for s in admitted], [s[0][1] for s in admitted], s = 25, color = 'red', edgecolor = 'k')

def display(m, b, color='g--'):
    plt.xlim(-0.05,1.05)
    plt.ylim(-0.05,1.05)
    x = np.arange(-10, 10, 0.1)
    plt.plot(x, m*x+b, color)

2. Lectura y representación gráfica de los datos

data = pd.read_csv('data.csv', header=None)
X = np.array(data0,1)
y = np.array(data[2])
plot_points(X,y)
plt.show()

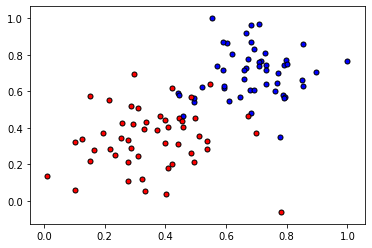
output_3_0.png

3. Implementación de las funciones básicas

  • Función de activación sigmoide

$$
\sigma(x) = \frac{1}{1+e^{-x}}
$$

  • Fórmula de salida (predicción)

$$
\hat{y} = \sigma(w_1 x_1 + w_2 x_2 + b)
$$

  • Función de error

$$
Error(y, \hat{y}) = – y \log(\hat{y}) – (1-y) \log(1-\hat{y})
$$

  • La función que actualiza los pesos

$$
w_i \longrightarrow w_i – \alpha (y – \hat{y}) x_i
$$
$$
b \longrightarrow b – \alpha (y – \hat{y})
$$

# Implement the following functions

# Activation (sigmoid) function
def sigmoid(x):
    return 1 / (1 + np.exp(x))

# Output (prediction) formula
def output_formula(features, weights, bias):
    return sigmoid(np.dot(features,weights) + bias)

# Error (log-loss) formula
def error_formula(y, output):
    return - y * np.log(output) - (1.-y) * np.log(1-output)

# Gradient descent step
def update_weights(x, y, weights, bias, learnrate):
    update = learnrate * (y - output_formula(x, weights, bias))
    weights -= update * x
    bias -= update
    return weights, bias

4. Función de entrenamiento
Esta función nos ayudará a iterar el algoritmo de descenso de gradiente a través de todos los datos, durante varias épocas. También trazará los datos y algunas de las líneas límite obtenidas a medida que ejecutamos el algoritmo.

np.random.seed(44)

epochs = 100
learnrate = 0.01

def train(features, targets, epochs, learnrate, graph_lines=False):
    
    errors = []
    n_records, n_features = features.shape
    last_loss = None
    weights = np.random.normal(scale=1 / n_features**.5, size=n_features)
    bias = 0
    for e in range(epochs):
        del_w = np.zeros(weights.shape)
        for x, y in zip(features, targets):
            output = output_formula(x, weights, bias)
            error = error_formula(y, output)
            weights, bias = update_weights(x, y, weights, bias, learnrate)
        
        # Printing out the log-loss error on the training set
        out = output_formula(features, weights, bias)
        loss = np.mean(error_formula(targets, out))
        errors.append(loss)
        if e % (epochs / 10) == 0:
            print("\n========== Epoch", e,"==========")
            if last_loss and last_loss < loss:
                print("Train loss: ", loss, "  WARNING - Loss Increasing")
            else:
                print("Train loss: ", loss)
            last_loss = loss
            predictions = out > 0.5
            accuracy = np.mean(predictions == targets)
            print("Accuracy: ", accuracy)
        if graph_lines and e % (epochs / 100) == 0:
            display(-weights[0]/weights[1], -bias/weights[1])
            

    # Plotting the solution boundary
    plt.title("Solution boundary")
    display(-weights[0]/weights[1], -bias/weights[1], 'black')

    # Plotting the data
    plot_points(features, targets)
    plt.show()

    # Plotting the error
    plt.title("Error Plot")
    plt.xlabel('Number of epochs')
    plt.ylabel('Error')
    plt.plot(errors)
    plt.show()

5. ¡Es hora de entrenar el algoritmo!

Cuando ejecutemos la función, obtendremos lo siguiente:

  • 10 actualizaciones con la pérdida de entrenamiento actual y la precisión
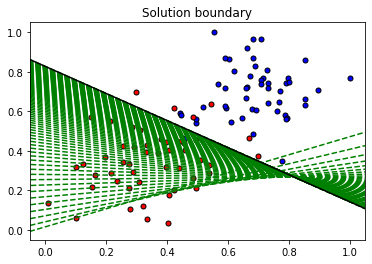
  • Un gráfico de los datos y algunas de las líneas de límite obtenidas. El último está en negro. Observa cómo las líneas se acercan cada vez más al mejor ajuste, a medida que pasamos por más épocas.
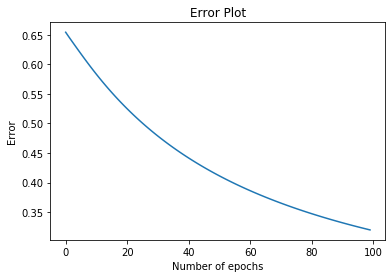
  • Un gráfico de la función de error. Observa cómo disminuye a medida que pasamos por más épocas.
train(X, y, epochs, learnrate, True)

========== Epoch 0 ==========
Train loss:  0.6542723014776058
Accuracy:  0.58

========== Epoch 10 ==========
Train loss:  0.5831565588208307
Accuracy:  0.68

========== Epoch 20 ==========
Train loss:  0.5248332996418759
Accuracy:  0.78

========== Epoch 30 ==========
Train loss:  0.4786495437763618
Accuracy:  0.85

========== Epoch 40 ==========
Train loss:  0.4415800012711709
Accuracy:  0.91

========== Epoch 50 ==========
Train loss:  0.41134852436963465
Accuracy:  0.93

========== Epoch 60 ==========
Train loss:  0.38631491067213325
Accuracy:  0.93

========== Epoch 70 ==========
Train loss:  0.36529302508807815
Accuracy:  0.93

========== Epoch 80 ==========
Train loss:  0.34741566773401744
Accuracy:  0.93

========== Epoch 90 ==========
Train loss:  0.3320399937351909
Accuracy:  0.93

output_9_1.png

output_9_2.png

Descenso del gradiente con errores cuadráticos

Una métrica habitual para calcular el error de nuestra predicción es la suma de los errores al cuadrado (SSE):

$$
E = \frac{1}{2} \sum_\mu \sum_j ( y_j^\mu – \hat{y}_j^\mu )^2
$$

donde $\hat{y}$ es la predicción e $y$ el valor verdadero; se toma la suma sobre todos los puntos de salidad $j$ y otra suma sobre todos los puntos de datos $\mu$.

Teniendo en cuenta que en una red neuronal la predicción depende de los pesos en la forma $\hat{y}\_j^\mu = f ( \sum\_i w\_{ij} x\_i^ \mu )$, la ecuación anterior se puede escribir como

$$
E = \frac{1}{2} \sum_\mu \sum_j ( y_j^\mu – f(\sum_i w_{ij}x_i^\mu ) )^2
$$

Nuestro objetivo será encontrar pesos $w\_{ij}$ que minimicen el error cuadrático $E$. Para hacer esto en una red neuronal se suele utilizar el descenso del gradiente.

El gradiente es simplemente la derivada parcial. Se trata de hacerlo mínimo en cada paso.

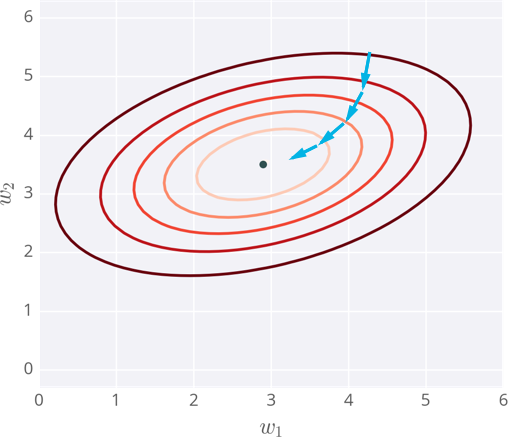
gradient-descent.png

Nota

Si los pesos se inicializan con los valores equivocados, el descenso del gradiente puede llevar a encontrar un mínimo local, no el mínimo global de la función.

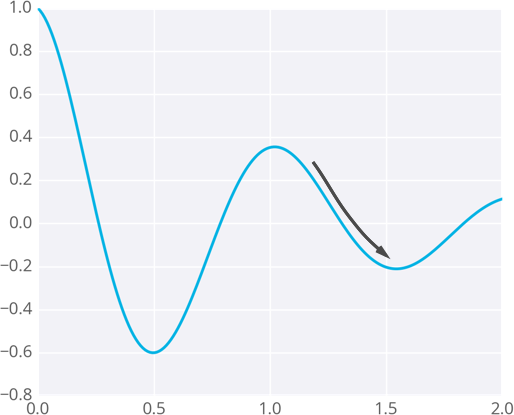
local-minima.png
Descenso de gradiente llevando a un mínimo local

Existen métodos para evitar este problema, como momentum.

Implementación del descenso del gradiente

Una actualización de peso se puede calcular como

$$
\Delta w_i = \eta \delta x_i
$$

siendo $\eta$ la tasa de aprendizaje y con el término de error $\delta$ como

$$
\delta =(y – \hat{y}) f'(h) = (y-\hat{y}) f'(\sum w_i x_i)
$$

Donde $(y – \hat{y})$ el error de salida, y $f'(h)$ es la derivada de la función de activación. A esta derivada se le llama gradiente de salida.

En el caso de una única unidad de salida, y utilizando como función de activación $f(h)$ el sigmoide, se tendría el siguiente código:

# Defining the sigmoid function for activations
def sigmoid(x):
    return 1/(1+np.exp(-x))

# Derivative of the sigmoid function
def sigmoid_prime(x):
    return sigmoid(x) * (1 - sigmoid(x))

# Input data
x = np.array([0.1, 0.3])
# Target
y = 0.2
# Input to output weights
weights = np.array([-0.8, 0.5])

# The learning rate, eta in the weight step equation
learnrate = 0.5

# the linear combination performed by the node (h in f(h) and f'(h))
h = x[0]*weights[0] + x[1]*weights[1]
# or h = np.dot(x, weights)

# The neural network output (y-hat)
nn_output = sigmoid(h)

# output error (y - y-hat)
error = y - nn_output

# output gradient (f'(h))
output_grad = sigmoid_prime(h)

# error term (lowercase delta)
error_term = error * output_grad

# Gradient descent step 
del_w = [ learnrate * error_term * x[0],
          learnrate * error_term * x[1]]
# or del_w = learnrate * error_term * x

Publicaciones Similares

  • Minería de datos

    Porroberto

    Definición de Minería de Datos La Minería de Datos (Data Mining) es un conjunto de técnicas y procesos de análisis de datos que permite extraer información de bases de datos y Almacenes de Datos mediante la búsqueda automatizada de patrones y relaciones. Modelos de Minería de Datos De verificación. El usuario solicita que se verifique…

  • Deep Learning

    Porroberto

    El aprendizaje profundo (deep learning) es un conjunto de algoritmos de aprendizaje automático (machine learning) basados en asimilar representaciones de datos. Una observación (por ejemplo, una imagen) puede ser representada en muchas formas (por ejemplo, un vector de píxeles), pero algunas representaciones hacen más fácil aprender tareas de interés (por ejemplo, "¿es esta imagen una…

  • Regresión logística

    Porroberto

    El algoritmo de regresión logística consiste en: Tomar los datos Elegir un modelo aleatorio Calcular el error Minimizar el error y obtener un modelo mejor

  • Feedforward

    Porroberto

    Se llama redes feedforward a las redes en que las salidas de una capa son utilizadas como entradas en la próxima capa. Esto quiere decir que no hay loops «hacia atrás». Siempre se «alimenta» de valores hacia adelante. El concepto de «fully connected Feedforward Networks» se refiere a que todas las neuronas de entrada, están…

  • Análisis de datos

    Porroberto

    En el Análisis de Datos (o Data Science) tenemos cinco etapas: Enmarcar el problema. Hacer las preguntas adecuadas.    – ¿Cuál es el objetivo?    – ¿Qué queremos estimar o predecir? Adquirir y preparar los datos.    – ¿Qué recursos tenemos para obtener datos?    – ¿Qué información es relevante?    – Limpiar y filtrar…

  • Almacén de datos

    Porroberto

    Definición de Almacén de Datos Un Almacén de Datos (o Data Warehouse) es una gran colección de datos que recoge información de múltiples sistemas fuentes u operacionales dispersos, y cuya actividad se centra en la Toma de Decisiones –es decir, en el análisis de la información– en vez de en su captura. Una vez reunidos…

Deja una respuesta

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *