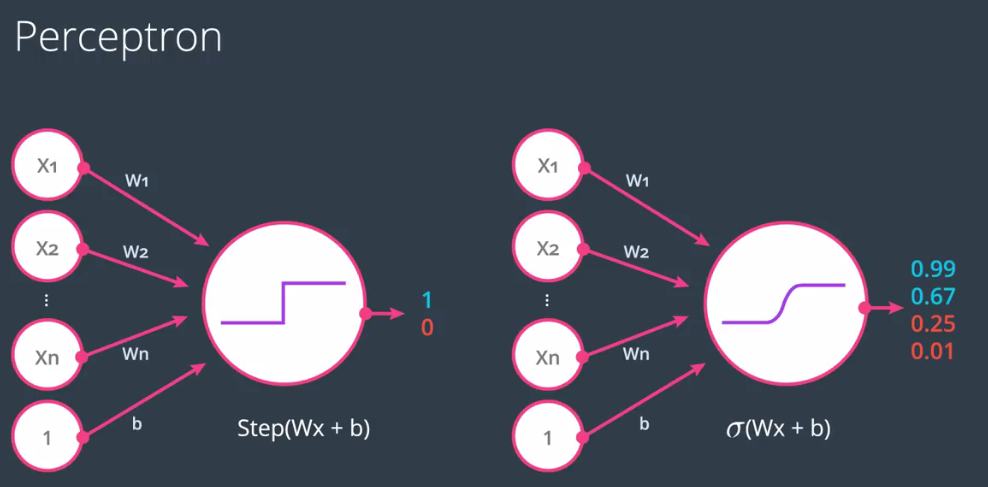
Perceptrón

El perceptrón es el bloque básico de construcción de las redes neuronales artificiales.

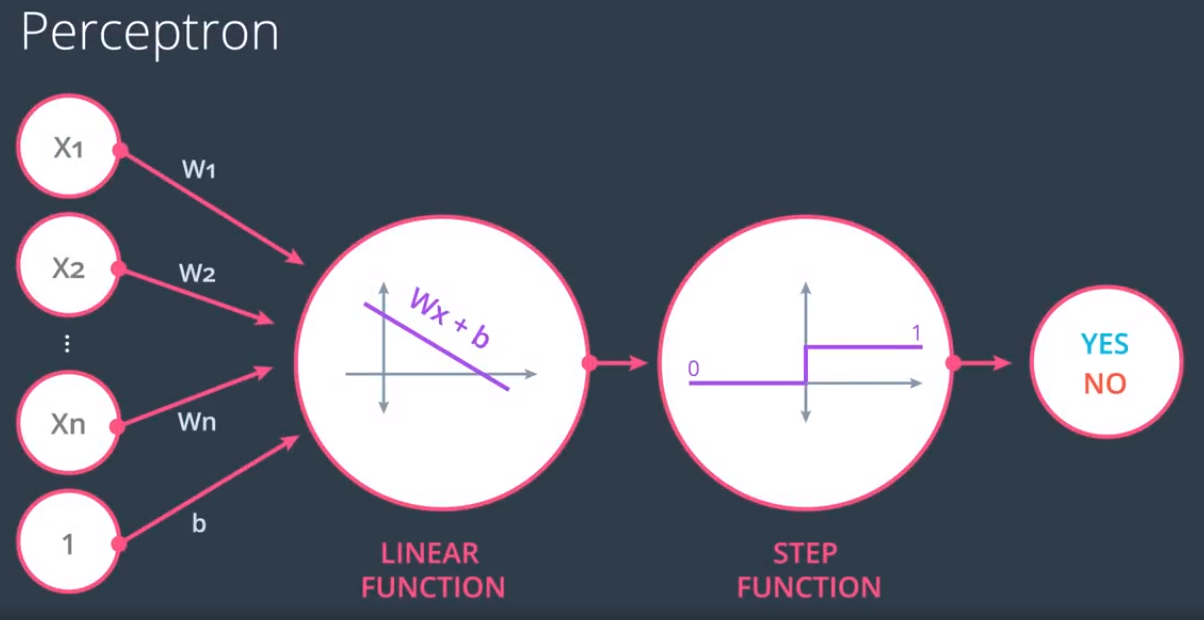
Los perceptrones se asemejan a las neuronas cerebrales.

Algoritmo lineal del perceptrón

Los pasos del algoritmo son los siguientes:

1. Inicializar los valores de los pesos y del bias (sesgo)
2. Propagar hacia delante
3. Comprobar el error
4. Retropropagar y ajustar pesos y sesgo
5. Repetir para todos los ejemplos de entrenamiento

Para ello se usa la siguiente predicción:

$$
\begin{aligned}
\mbox{Predicción } y' & = 1 \mbox{ si } Wx+b>0 \\
& = 0 \mbox{ si } Wx+b\leq 0
\end{aligned}$$

La forma de utilizar el algoritmo es:

1. Comenzar con valores aleatorios de los pesos $w_1, \dots, w_n$ y del sesgo $b$.
2. Para cada punto clasificado incorrectamente $x_1, \dots, x_n$:
   1. Si $\mbox{Predicción } = 0$:
      • Para cada $i = 1, \dots, n$
        • $w_i \leftarrow w_i + \alpha x_i$
      • $b \leftarrow b + \alpha$
   2. Si $\mbox{Predicción } = 1$:
      • Para cada $i = 1, \dots, n$
        • $w_i \leftarrow w_i - \alpha x_i$
      • $b \leftarrow b - \alpha$

Donde $\alpha$ será un valor suficientemente pequeño, denominado tasa de aprendizaje.

Perceptrones como operadores lógicos

Algunos operadores lógicos, como AND, OR y NOT, se pueden representar como perceptrones.

AND

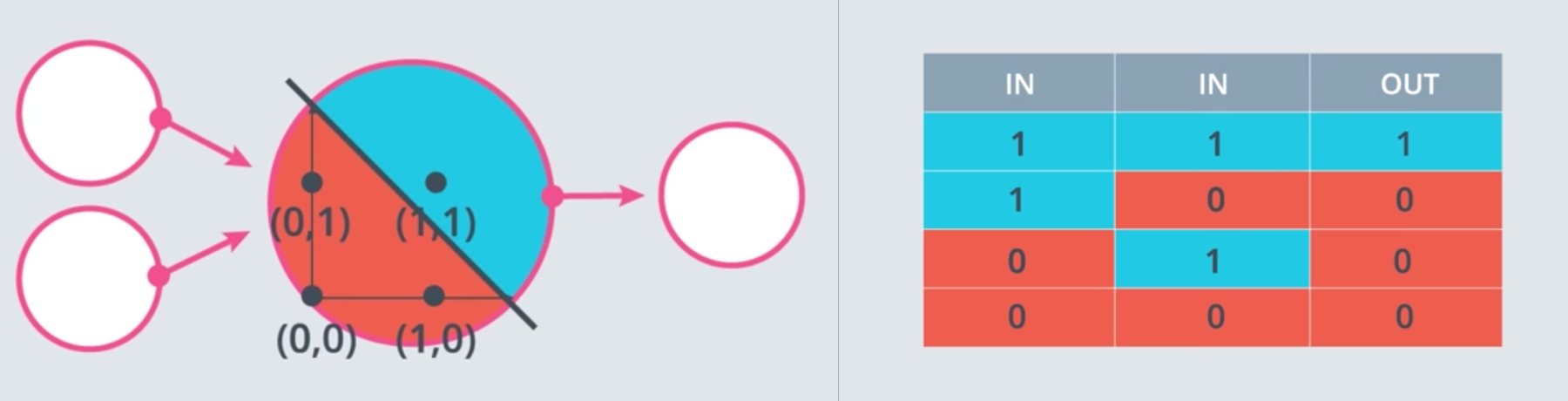
Buscamos qué valores podemos usar para la matriz de pesos y el sesgo.

Primer caso: $(0, 0)$

• De $w_1\cdot x_1\cdot w_2\cdot x_2+b$, inicializando $w_1=w_2=1, b=-1$, tenemos $ 1\cdot x_1 + 1\cdot x_2-1$
• Pasando el primer punto $(x_1=0,x_2=0)$ tenemos $0+0-1=-1$
• De la regla del perceptrón, si $Wx+b\leq 0$, entonces $y'=0$, que coincide con la salida de la puerta AND. Por tanto este caso es correcto, y no se necesita volver para atrás.

Segundo caso: $(0,1)$

• Pasando el punto $(x_1=0,x_2=1)$ tenemos $0+1-1=0$
• De la regla del perceptrón, si $Wx+b\leq 0$, entonces $y'=0$, que coincide con la salida de la puerta AND. Por tanto este caso es correcto, y no se necesita volver para atrás.

Tercer caso: $(1,0)$

Igual que el anterior.

Cuarto caso: $(1,1)$

• Pasando el punto $(x_1=1,x_2=1)$ tenemos $1+1-1=1$
• De la regla del perceptrón, si $Wx+b> 0$, entonces $y'=1$, que coincide con la salida de la puerta AND. Por tanto este caso es correcto, y no se necesita volver para atrás.

Por tanto los valores para la matriz de pesos $W=(1,1)$ y el bias $b=-1$ son válidos para la puerta AND.

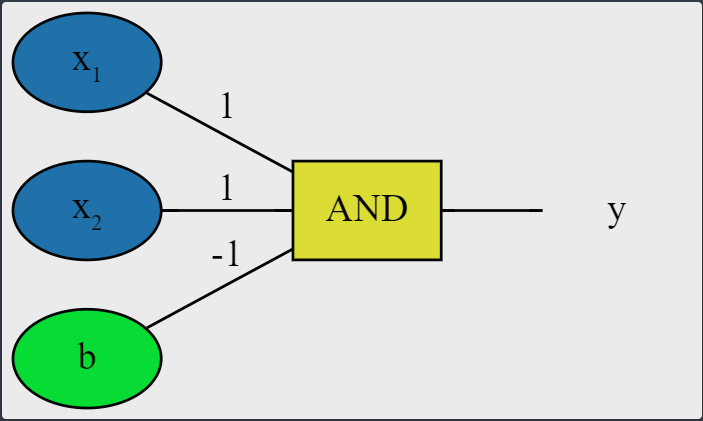
OR

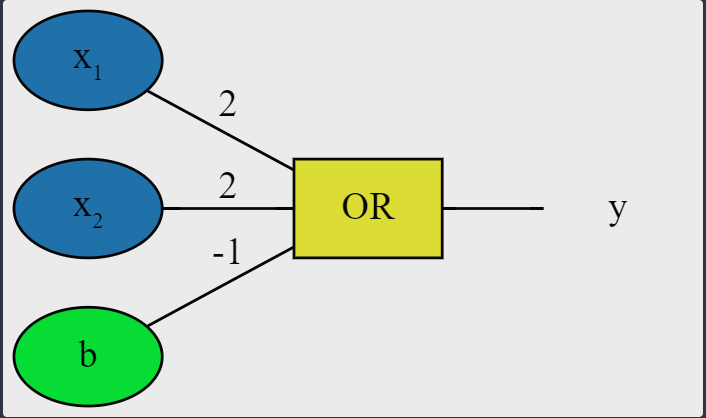
A igual que antes, buscamos qué valores podemos usar para la matriz de pesos y el sesgo.

Primer caso: $(0, 0)$

• De $w_1\cdot x_1\cdot w_2\cdot x_2+b$, inicializando $w_1=w_2=1, b=-1$, tenemos $ 1\cdot x_1 + 1\cdot x_2-1$
• Pasando el primer punto $(x_1=0,x_2=0)$ tenemos $0+0-1=-1$
• De la regla del perceptrón, si $Wx+b\leq 0$, entonces $y'=0$, que coincide con la salida de la puerta OR. Por tanto este caso es correcto, y no se necesita volver para atrás.

Segundo caso: $(0,1)$

• Pasando el punto $(x_1=0,x_2=1)$ tenemos $0+1-1=0$
• De la regla del perceptrón, si $Wx+b\leq 0$, entonces $y'=0$, que no coincide con la salida de la puerta OR.
• Cambiamos el valor de $w_2$ a 2 entonces tenemos:
  • Para $(0,0)$, $0+0-1=-1<0$, correcto.
  • Para $(0,1)$, $0+2-1=1>0$, correcto.

Tercer caso: $(1,0)$

• Pasando el punto $(x_1=1,x_2=1)$ tenemos $1+0-1=0$
• De la regla del perceptrón, si $Wx+b\leq 0$, entonces $y'=0$, que no coincide con la salida de la puerta OR.
• Cambiamos el valor de $w_1$ a 2 entonces tenemos:
  • Para $(0,0)$, $0+0-1=-1<0$, correcto.
  • Para $(0,1)$, $0+2-1=1>0$, correcto.
  • Para $(0,1)$, $2+0-1=1>0$, correcto.

Cuarto caso: $(1,1)$

• Pasando el punto $(x_1=1,x_2=1)$ tenemos $2+2-1=3$
• De la regla del perceptrón, si $Wx+b> 0$, entonces $y'=1$, que coincide con la salida de la puerta OR. Por tanto este caso es correcto, y no se necesita volver para atrás.

Por tanto los valores para la matriz de pesos $W=(2,2)$ y el bias $b=-1$ son válidos para la puerta OR.

Otras puertas lógicas

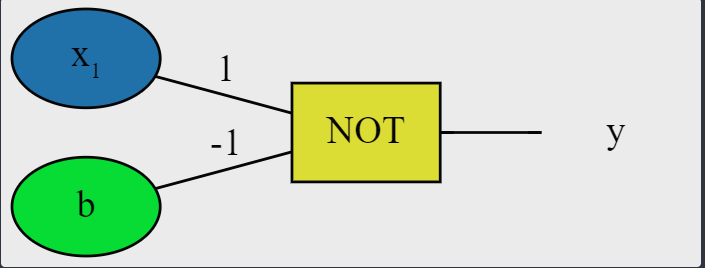
Perceptrón NOT

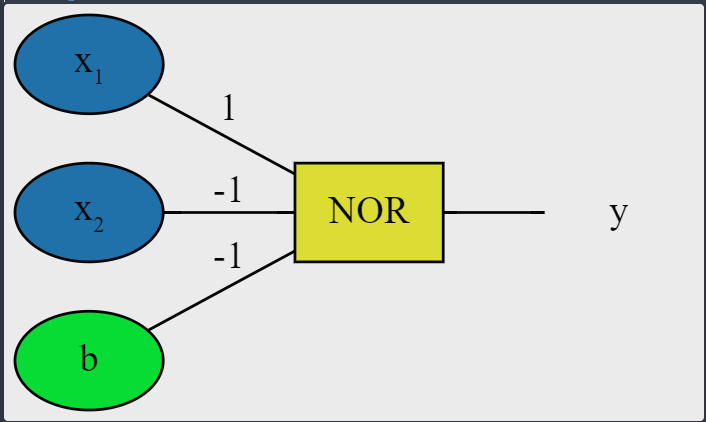
Perceptrón NOR

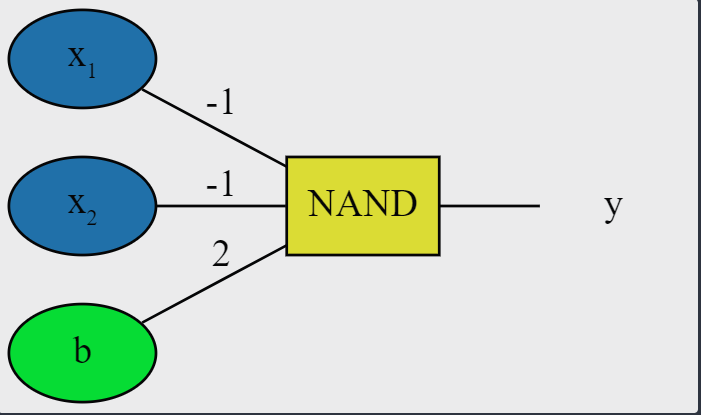
Perceptrón NAND

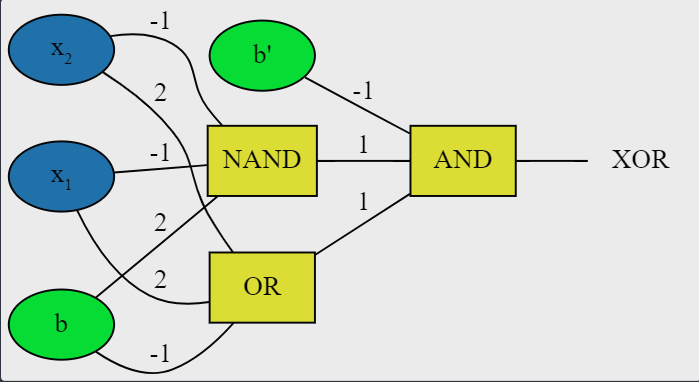
Red neural XOR combinando perceptrones

Función de error

En los problemas de clasificación se trata de minimizar la función de error.

En la optimización las funciones de error continuas son mejores que las discretas.

Algoritmo continuo del perceptrón

Para conseguir un algoritmo con una función continua en vez de discreta, lo que se hace es cambiar la función de paso por una función continua equivalente, la sigmoide, definida por

$$
\sigma(x) = \frac{1}{1+e^{-x}}
$$