Redes neuronales
Las redes neuronales se utilizan para el aprendizaje profundo, o Deep Learning.
El diseño de las Redes Neuronales Artificiales está inspirado en las redes neuronales biológicas, imitando la forma en que opera el cerebro. Las neuronas utilizadas en las redes artificiales básicamente son funciones matemáticas.
Cada red tiene:
- Neuronas de entrada, capa de entrada de neuronas
- Neuronas de salida, capa de salida de neuronas
- Neuronas internas, capas ocultas de neuronas
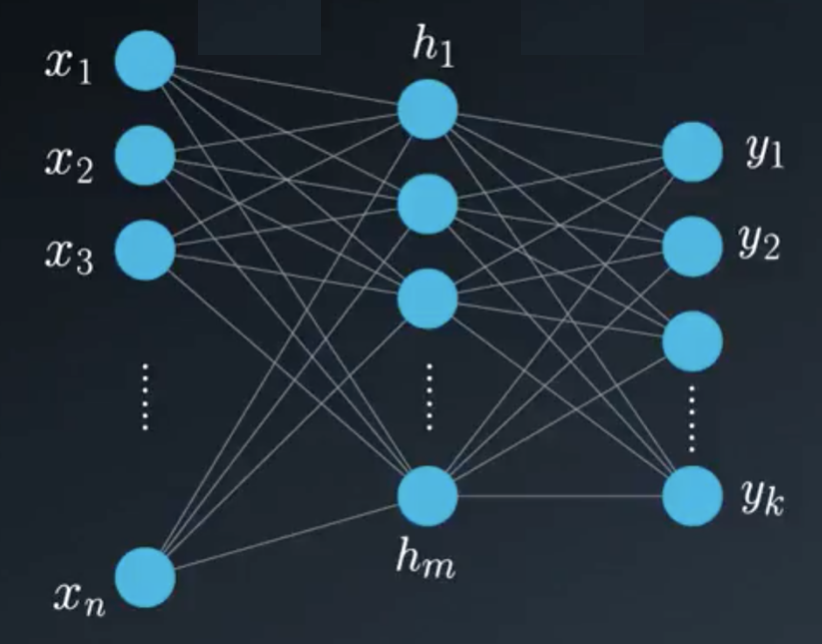
Red neuronal artificial simplificada
En la figura anterior se ve una red neuronal compuesta por:
- Un vector de entrada $\vec{x} = [x_1, x_2, x_3, \dots, x_n]$
- Un vector interno oculto $\vec{h} = [h_1, h_2, h_3, \dots h_n]$
- Un vector de salida $\vec{y} = [y_1, y_2, y_3, \dots y_n]$
Las líneas simbolizan un coeficiente(escalar) que conecta una neurona a la siguiente. Estos coeficientes se llamnan pesos. Como hay demasiados pesos conectando una capa con la siguiente, estos coeficientes se organizan en una matriz llamada matriz de pesos.
Al trabajar con redes neuronales se tienen dos fases principales:
- Entrenamiento
- Avance
- Retropropagación
- Evaluación
Durante la fase de entrenamiento se toma el conjunto de datos y se busca el mejor conjunto de pesos que nos den el resultado deseado.
En la fase de evaluación se trabajo con la red creada en la fase de entrenamiento, aplicando nuestras entradas y esperando obtener el resultado deseado.
Estos pasos se repiten las veces necesarias.
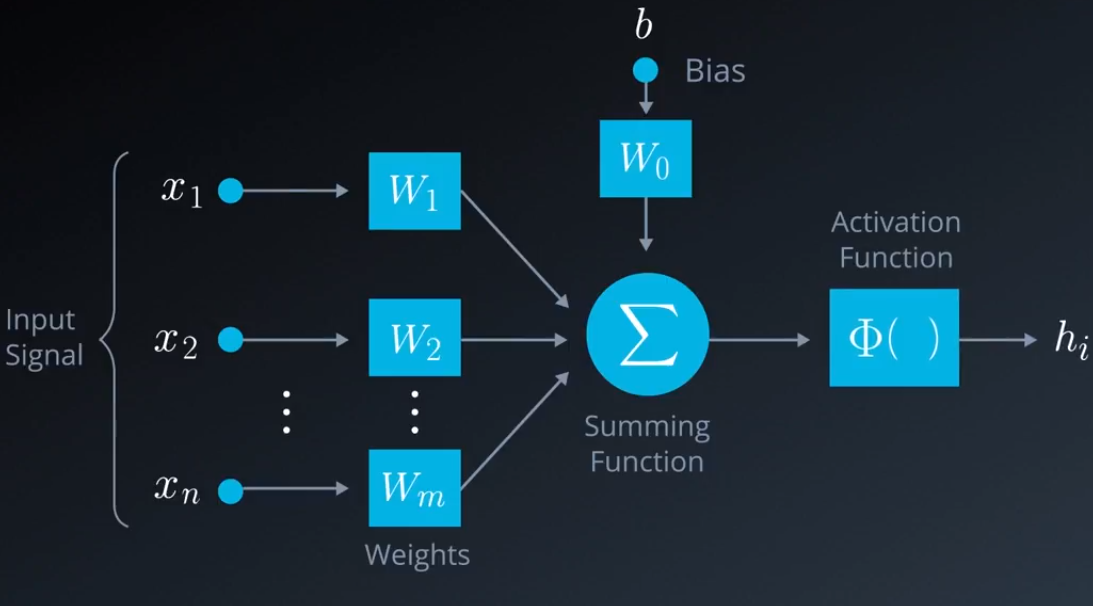
Fase de entrenamiento
